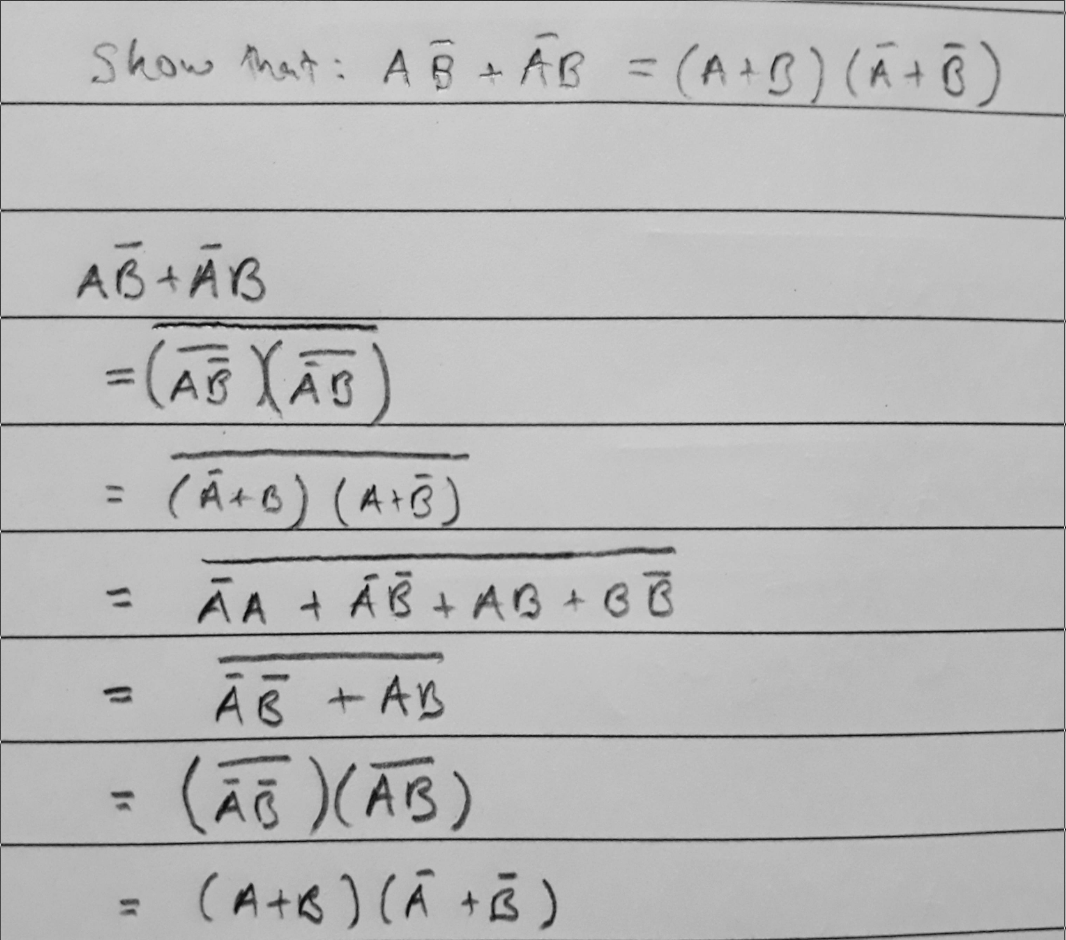ALevel
6.5 - Boolean Algebra
- like Maths Algebra - follow certain rules
-
Boolean operators
- \(+\) addition:
OR - \(\cdot\) multiplaction:
AND - \(\overline{}\) overline:
NOT. AKA: Inversion, complement, negation, etc
- \(+\) addition:
- NB: AND has greater precedence than OR
Boolean Identities and Laws:
| Name | AND Form | OR Form |
|---|---|---|
| Identity Law | \(1A=A\) | \(0+A=A\) |
| Null Law | \(0A=0\) | \(1+A=1\) |
| Idempotent Law | \(AA=A\) | \(A+A=A\) |
| Inverse Law | \(A\overline{A}=0\) | \(A+\overline{A}=1\) |
| Commutative Law | \(AB=BA\) | \(A+B=B+A\) |
| Associative Law | \((AB)C=A(BC)\) | \((A+B)+C=A+(B+C)\) |
| Distributive Law | \(A+BC=(A+B)(A+C)\) | \(A(B+C)=AB+AC\) |
| Absorption Law | \(A(A+B)=A\) | \(A+AB=A\) |
| De Morgan’s Law | \(AB=\overline{\overline{A}+\overline{B}}\) | \(A+B=\overline{\overline{A}\cdot\overline{B}}\) |
| Double Negation | \(\overline{\overline{A}}=A\) |
Null Law
\(0A=0\): Let’s say whether I am allowed to eat things that are red is \(A\) (yes/no). And whether I am able to eat ice cream is \(0\) (= not allowed). Am I allowed to eat red ice-cream? No.
\(1+A=1\). (Something that is always true) OR A. Here, A is irrelevant, you don’t even need to bother ORing. The answer is of course going to be true.
Distributive Law
\(A(B+C)=AB+AC\) makes sense in traditional algebra as well. \(A+BC=(A+B)(A+C)\) is unique to boolean algebra though. Basically don’t forget works with + operator too.
Absorption Law
\(A(A+B)=A\). If \(A\) is true, the part inside the brackets are true as well. If \(A\) is false, the expression, would be \(0(A+B)=0\) (Null law). So clearly \(B\) is irrelevant and the expression is equivalent to \(A\).
\(A+AB=A\): If \(A\) is \(1\), then since for OR gates, we only need one of the inputs to be true, the output is clearly \(1\), without even having to think about the rest. If \(A\) is \(0\), since the output of an AND gate will always be \(0\) if any of the inputs are \(0\), we also know that the output will be \(0\) without having to think any further. Evidently, \(A+AB=A\)
De Morgan’s Law
Might be tricky seeing how this scales up when you have multiple variables by just looking at it algebraically. I feel it is best expressed as an algorithm:
Consider an expression made out of smaller expressions (let’s call them “smalls”), all with the same operator between them (\(\cdot\) or \(+\)). E.g: for \(A+B+C\), the smalls are \(A\),\(B\) and \(C\) (and the operator is \(+\)).
- NOT all smalls
- Switch all operators
- NOT the whole expression
Clarification: “switch all operators” means, replace all \(\cdot\)s with \(+\) and \(+\)s with \(\cdot\)s.
Caution with NOTs
NOT(A AND B) is not (NOT A) AND (NOT B) !
\[\overline{AB}\neq\overline{A}\cdot\overline{B}\]If we take De Morgan’s law and NOT both sides, we can actually see that:
\[\overline{AB}=\overline{A}+\overline{B}\]Don’t get mixed up!
Also:
| Expression | = | Cancellation Possible? |
|---|---|---|
| \(\overline{\overline{A+B}}\) | \(A+B\) | Yes |
| \(\overline{\overline{A}}+\overline{\overline{B}}\) | \(A+B\) | Yes |
| \(\overline{\overline{A}\cdot\overline{B}}\) | \(\overline{\overline{A}\cdot\overline{B}}\) | No |
| \(\overline{\overline{\overline{A}\cdot\overline{B}}}\) | \(\overline{A}\cdot\overline{B}\) | Yes |
Worked Examples