For my bubble trouble game, I decided I wanted to have heart shapes to indicate lives at the top of the screen. I’m writing the game from scratch though, using nothing other than the JavaScript canvas scripting API - and of course it’s not like there’s just a built-in function that you can call and it’ll draw you a heart. Who knew I’d spend almost an entire day working on this one aspect though…

There’s a couple of ways you could go about drawing heart-shapes:

1. Just use a sprite image
2. Bezier curves !
3. Graphing equations

Sprites

First of all, I’m dismissing option 1. straight away: right now, my game is just two neat little files: bubbletrouble.js which is the script, and index.html which literally just defines a canvas and loads the script - and I want to keep it that way. I don’t really want to introduce an extra assets folder to the mix with sprite images or something like that - besides, that isn’t really my style (if you’ve seen some of my other games, you know what I mean).

Bezier

As for Bezier curves, I’m a real fan of them so they could be a way to go. The following is an example of a heart drawn with some quadratic bezier curves. One look at those strange rounded tops of the heart, though, and I feel like I can do better. Moving swiftly on to graphing equations…

Graphing Equations

This is basically the focus of this article, and it’s what I experimented around with the most. I found a couple of heart equations on Wolfram MathWorld and here are two I liked…

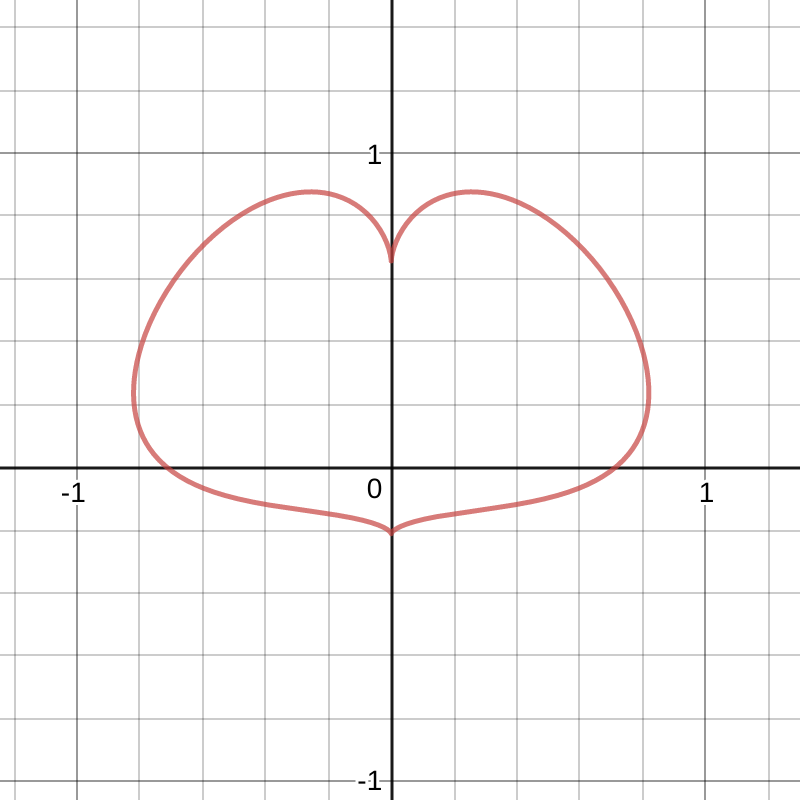
Equation 1

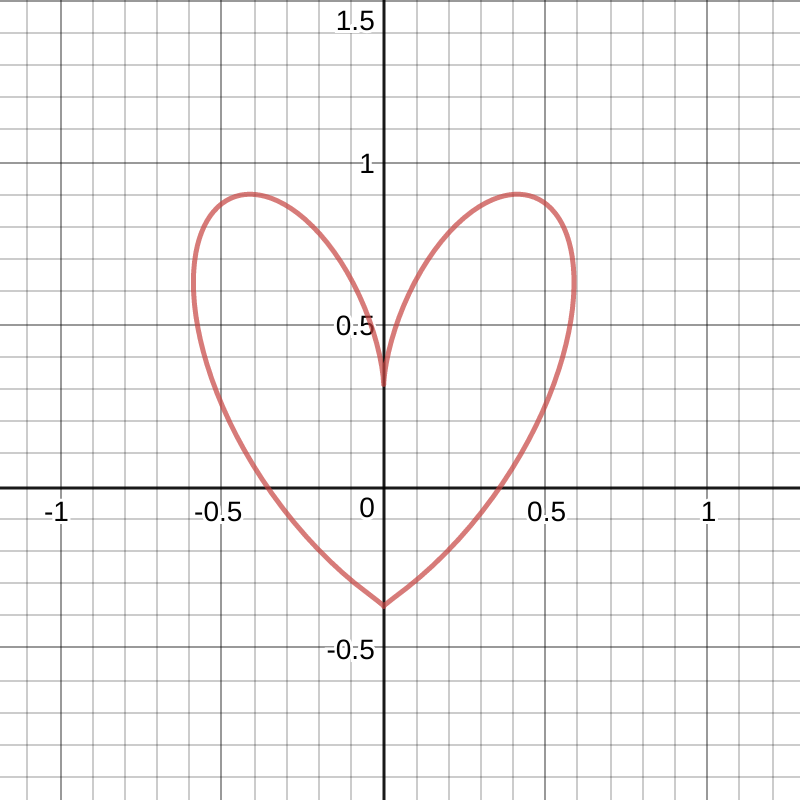
This equation is quite neat. The intersection points with the axes are at nice values and it probably looks the best out of all the hearts here.

I first rearranged the equation into a \(y=f(x)\) form so that I can graph it easier with code:

This is the rearranged version:

Here’s how I implemented the drawing of this equation:

/**
 * @param s size
 */
function drawHeart(x,y,s){
    /**
     * @param n negative sqrt version or not
     */
    function f(x,n=false){
        var ret = Math.pow(x,2/3);
        var part = Math.pow(Math.pow(x,4/3)-4*(x*x-1),1/2);
        
        if(n){
            part*=-1;
        }
        
        return (ret+part)/2;
    }

    function path(n=false){
        for(var i=-1.2*s+x;i<1.2*s+x;i+=s/2000){
            var id = ((1/s)*i)-(x/s); // i dash: i with transformations applied
            var j = -s*f(id,n)+y;
            if(n){
                j-=s/40; // discontinuity correction
            }
            cx.fillRect(i,j,1,1); // draw pixel at (i,j)
        }
    }

    // top
    path(false); // false = positive sqrt

    // bottom
    path(true); // true = negative sqrt
}

Note:
The equation has a \(\pm\) so I had to split the drawing into two parts: one where I take the positive sqrt (red) and one where I take the negative sqrt (blue) for that bit in the equation. Guess it takes two halves to draw a heart :) ^{(they’re not halves area-wise though)}

Other notes:

1. The ‘discontinuity correction’ refers to an adjustment I made to move the bottom part up slightly so that it looks like the two parts are more connected.
2. The y coordinate is flipped because the coordinate system is such that the origin is the top-left in JavaScript (usually the case with programs)
3. I do some transformations (see the variable ‘id’) so that the drawing takes into account the specified x and y locations as well as the ‘s’ (size multiplier) variable
4. The domain of the equation is taken roughly to be \(-1.2<x<1.2\)
5. The ‘s’ variable is divided by 2000 to approximately convert the unit of ‘s’ to pixels.

Here is the result:

Wait … what? I was so confused. Did I do something wrong rearranging? Some other error?

After a bunch of debugging, I found out that something strange was happening with the built-in Math.pow function itself. The following image is an observation I made which sums it up:

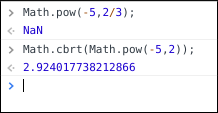
I’d been taught in school, etc, that these two were the same thing. I remember learning the equation

What’s more, my (physical) calculator gives the answer I expected for that same exact question (as does the graphing software, desmos, I used to make those graph images above).

Calculating the same thing in Python gives an even more interesting result.

This result basically confirmed my suspicion that while I was here minding my business, trying to draw some hearts, I had inadvertently grazed the complex realm - which is actually pretty awesome.

Looking around, it turns out it’s actually in the ECMAScript specification that Math.pow should return NaN in situations like this (negative base, non-integer exponent).

Also, looking around on WolframAlpha, I found out that the equation I had learnt in school (mentioned earlier) essentially had the caveat that we were taking the real valued root.

Note that in this situation, we are essentially cubing a negative number: .

Now, this is my first time ever coming across complex numbers, but I’m going to try explain what is going on with my understanding from what I’ve been reading. In this situation, there are actually three solutions, it’s just that one of them is real and the other two are complex.

We can plot these on a graph with the horizontal axis being real numbers and the vertical axis being imaginary (-1j,0,1j,2j,..). Here they are for this situation:

Notice how the blue solution lies exactly on the horizontal axis - this means that it doesn’t have an imaginary part and so is a real number. This real solution (2.924…) is what my calculator gets.

The problem with \(\frac{2}{3}\) is that JavaScript doesn’t store fractions like that at all: it first has to convert it into its decimal representation. The decimal representation in this case is non-terminating though: it’s \(0.66666...\). Of course we can’t store an infinite amount of decimal places so this number is truncated at some point.

Technically this means that there will always be a very very slight inaccuracy when working with any kind of fraction like this in most programming languages, but that inaccuracy is so tiny that we don’t have to worry about it too much at all - especially when we’re only dealing with real numbers.

So in other words, when we try to calculate \((-5)^{\frac{2}{3}}\) in JavaScript, what it’s actually trying to do is \((-5)^{0.6666666666666666}\) which is of course going to be super super close to what we want, but not exactly.

The problem is that this slight difference means that our solutions as shown in that diagram above get rotated a very very slight amount about the origin and also a lot of new solutions will be introduced as well. At the end of the day, none of these will lie exactly on the horizontal axis, and so there are no real solutions.

Well dealing with complex numbers seems to be outside the scope of a simple browser language like JavaScript - and trying to guess real solutions close to the actual solutions seems to be beyond it as well. These considerations must have been why it was decided that JavaScript should just return NaN for difficult cases like this.

Python (version 3) actually can handle complex numbers, however, and it turns out that the solution it gave earlier was the red solution - a solution known as the principal solution, and there’s probably some good reasoning behind why it gave that one and not the blue one, for example (which I’ll probably find out more about when I look at complex numbers in greater detail in future).

Reaching this explanation (although I’m not 100% sure about it), I am reasonably satisfied with my understanding of what’s going on. The problem remains though: how do I actually fix the heart drawing.

Well, the problem essentially arises from the fact that \(\frac{2}{3}\) can’t exactly be represented as decimal. To get around this, I decided to not evaluate the fraction straight away, and instead incorporate the numerator and denominator directly into our calculations. I.e: create a function which takes the three inputs \((x,m,n)\) corresponding to a value of the form \(x^{\frac{m}{n}}\) and returns the real solution.

Well of course, using the equation from earlier, , we can implement this by simply taking the n-th root of \(x^m\) as long as that root function is the real root. Luckily, JavaScript has Math.sqrt and Math.cbrt which can find the real root of something when it is square rooted or cube rooted (when n is 2 or 3) - that’s why Math.cbrt worked earlier. JavaScript hasn’t got a n-th root function though, because again, that seems to be beyond the scope of a simple language - and cube rooting and square rooting is the most people usually need to worry about.

This basically means that if I rewrite my heart equation as the following, I should be able to implement it in JavaScript making use of the Math.cbrt function:

To me, this didn’t seem satisfactory though. Sure, in this case, it works out because I end up not having to use anything more than the cube root, but it could have easily been otherwise. What if I wanted to compute ?

Basically, leaving that function I was talking about as something like the following didn’t feel satisfactory to me at all:

/**
 * @param x base
 * @param m exponent numerator
 * @param n exponent denominator
 */
function pow(x,m,n){
    if(n==1){
        return Math.pow(x,m);
    }
    else if(n==2){
        return Math.sqrt(Math.pow(x,m));
    }
    else if(n==3){
        return Math.cbrt(Math.pow(x,m));
    }
    else{
        // what do...?
    }
}

Well, I thought about how to emulate my calculator a little and this is what I observed:

As long as when \(x<0\), \(n\) is even (otherwise my calculator gives a math error). Where sign(x) is a function which returns \(-1\) if \(x<0\) and \(1\) if \(x>0\) (and \(0\) if \(x=0\)).

And here’s how I implemented this in code:

function pow(x,m,n){
    if(x<0 && n%2==0){
        return NaN;
    }
    return Math.pow(Math.sign(x)*(Math.pow(Math.abs(x),1/n)),m);
}

There, that’s much better. There’s probably an even nicer way of expressing this though, and I haven’t thought about special cases that much (such as when \(x=0\) or \(n=0\)) but this does the job very nicely for my application (I’ll think about those later).

Tweaking the code slightly to work with this new function instead of Math.pow, we can now successfully draw the heart !

Final code:

/**
* @param x base
* @param m exponent numerator
* @param n exponent denominator
*/
function pow(x,m,n){
    if(x<0 && n%2==0){
        return NaN;
    }
    return Math.pow(Math.sign(x)*(Math.pow(Math.abs(x),1/n)),m);
}


/**
* @param s size
*/
function drawHeart(x,y,s){
    /**
    * @param n negative sqrt version or not
    */
    function f(x,n=false){
        var ret = pow(x,2,3);
        var part = pow(pow(x,4,3)-4*(x*x-1),1,2);
        
        if(n){
            part*=-1;
        }
        
        return (ret+part)/2;
    }

    function path(n=false){
        for(var i=-1.2*s+x;i<1.2*s+x;i+=s/2000){
            var id = ((1/s)*i)-(x/s); // i dash: i with transformations applied
            var j = -s*f(id,n)+y;
            if(n){
                j-=s/40; // discontinuity correction
            }
            cx.fillRect(i,j,1,1);
        }
    }

    // top
    cx.fillStyle = '#F25F5C';
    path(false); // false = positive sqrt

    // bottom
    cx.fillStyle = '#247BA0';
    path(true); // true = negative sqrt
}

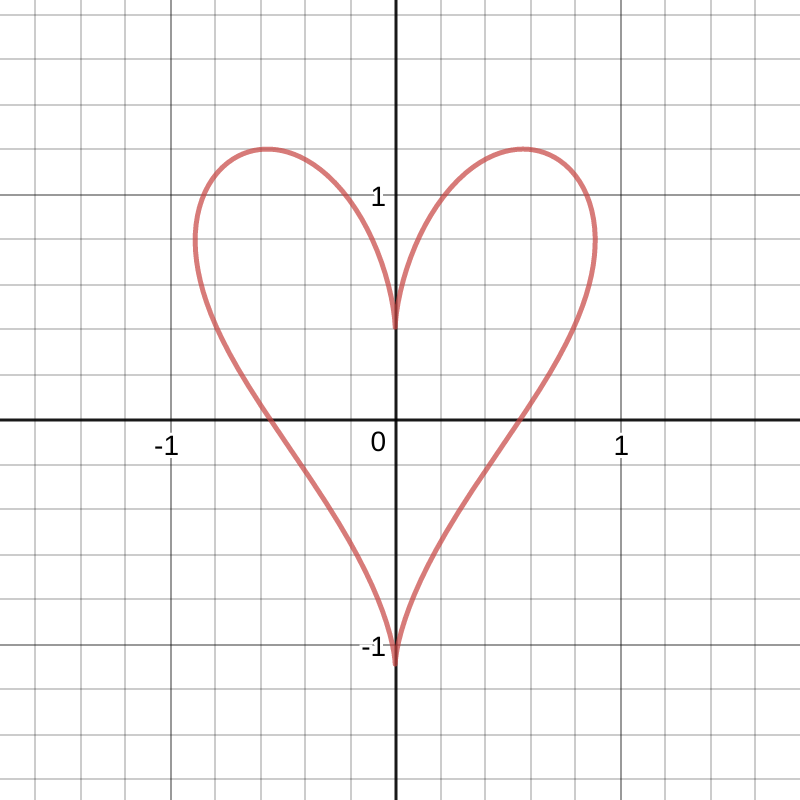
Equation 2

After stumbling across the complex realm and spending almost the whole day with this equation, I finally have reached a satisfactory point ! Now I have my heart, and everything’s complete ! … Well, not quite - because I then decided to take a look at another heart equation as well.

This equation doesn’t look as pretty as the first equation - it’s got a bunch of constants everywhere. The graph doesn’t look as good as the first equation either, i’d say, but it’s still pretty good. Also, it doesn’t have nice intersection points with the axis like the first equation - instead, I manipulated those to be nicer by altering some constants (applying some transformations).

But even so, honestly, I do really like this equation. Sure, it’s got a bunch of mysterious numbers, but the results you can get by playing around with the constants are awesome - and that’s one of the best things about it ! Have a go for yourself below (or at this link):

Click to reveal some cool shapes I made just by altering some of the constants:

Shapes Showcase

The cool heart shape ~ It does indeed look pretty cool ^{thanks for always letting me rant about random stuff like this to you btw :)} blub pointier Looks more hand-drawn-like Looks more like equation 1 - actually looks really good Resembles a petal-like shape (maybe rose petals)

Another thing about this equation is that it is a parametric equation. \(t\) is the parameter, and its range is \(0\leq t \leq 2\pi\).

The fact that it is a parametric equation makes drawing the graph for it in code a lot easier, because it means I just need to interpolate a variable \(t\) across that range and plot a point at the x and y coordinates as described by the equation for each value of \(t\).

In fact, for the first equation, in some sense, when I rearranged it, I was essentially putting it into a parametric form because any curve given in the form \(y=f(x)\) can be written in the parametric form: \((x,y)=(t,f(t))\) where the range of \(t\) is the domain of the function \(f(x)\).

The code for drawing this curve is so simple, having just gone through everything with equation 1:

/**
* @param s size
*/
function drawHeart(x,y,s){
    var a = 0.0769;
    for(t=0;t<2*Math.PI;t+=0.001){
        var i = 0.5*s*a*15.7*Math.pow(Math.sin(t),3)+x;
        var j = -0.5*s*a*(15.7*Math.cos(t)-5*Math.cos(2*t)-2*Math.cos(3*t)-Math.cos(3*t))-5+y;
        cx.fillRect(i,j,1,1); // plot pixel at coord (i,j)
    }
}

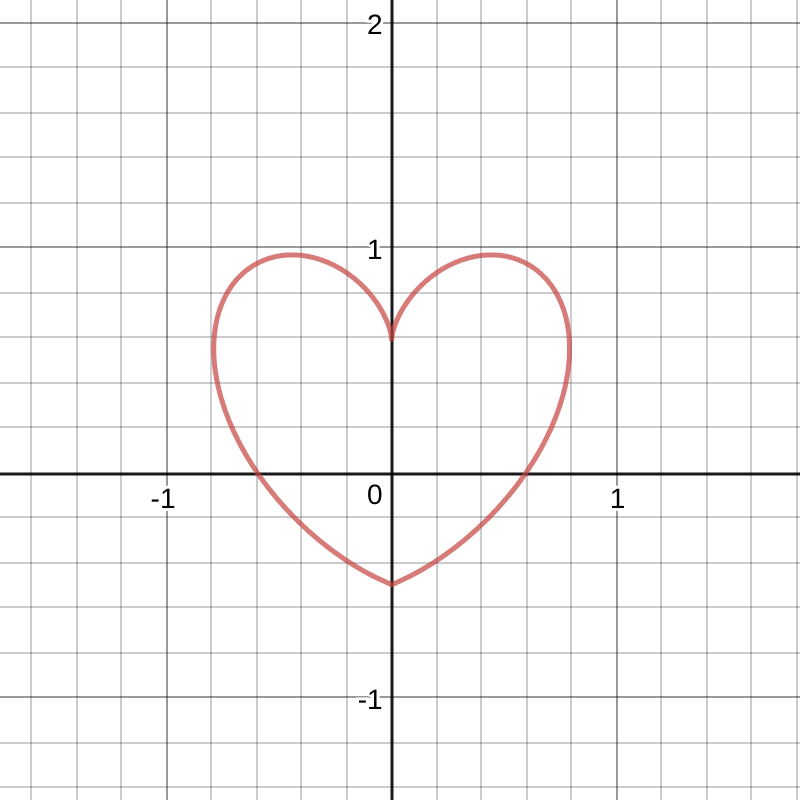
It’s essentially a direct translation of the math into code - with just some minor tweaking so that the function takes into account the given \((x,y,s)\) parameters. It was so easy to implement. I barely had to think about it at all - didn’t have to think about complex numbers, didn’t have to deal with splitting up the equation into different parts, didn’t even have to rearrange - and it just works. First time. Below is the above code in action:

If we edit the code so that rather than plotting pixels, we plot a path - using the lineTo function part of the canvas API, we can let the API do some anti-aliasing and the result is beautiful.

function drawHeart(x,y,s){
    cx.beginPath();
    var a = 0.0769;
    for(t=0;t<2*Math.PI;t+=0.001){
        var i = 0.5*s*a*15.7*Math.pow(Math.sin(t),3)+x;
        var j = -0.5*s*a*(15.7*Math.cos(t)-5*Math.cos(2*t)-2*Math.cos(3*t)-Math.cos(3*t))-5+y;
        cx.lineTo(i,j);
    }
    cx.closePath();
    cx.stroke();
}

Remember how I said how the constants in the equation is one of the best things about it? Well the rest of this space shall now be dedicated to various experiments regarding them ! (Also, you can see the code for everything by looking at the source code of this page)

I could go on. There’s so many cool patterns you can create with this equation - it really is amazing ! You can try messing around with the code and seeing what you can create yourself:

Conclusion

I don’t want to be too dramatic but after this, I don’t think I’ll ever look at hearts the same again. Honestly.

Seeing how equation 2 took me about 5 minutes to implement and equation 1 took (let’s just say) quite a bit longer, it might seem easy to dismiss looking at equation 1 as a waste of time - but I know that’s not true at all. I wouldn’t have found out all this interesting stuff about complex numbers otherwise. Equation 1 was super interesting and that’s justification enough. (They both were super interesting actually).

As for which of these equations I’ll actually end up using for my game, bubbletrouble, (that’s what this was all about, remember?)… I haven’t made my mind up yet - they’re both really cool and beautiful. To be honest, I’m hovering more towards the equation 2 side though :P

Thanks for reading, and I hope you found these hearts as interesting as I did!